Why We Need the Theory of Sampling

The purpose of sampling is to extract a representative amount of material from a ‘lot’ – the ‘sampling target’. It is clear that sampling must and can only be optimized before analysis. In a recent paper, we show how non-representative sampling processes will always result in an invalid aliquot for measurement uncertainty (MU) characterization (1).

A specific sampling process can either be representative – or not. If sampling is not representative, we have only undefined, mass-reduced lumps of material without provenance (called ‘specimens’ in the theory of sampling) that are not actually worth analyzing. Only representative aliquots reduce the MU of the full sampling-and-analysis process to its desired minimum; and it is only such MU estimates that are valid. Sampling ‘correctness’ (which we define later) and representativity are essential elements of the sampling process.

TOS Versus MU in Brief

Current Measurement Uncertainty (MU) approaches do not take sufficient account of all sources affecting the measurement process, in particular the impact of sampling errors. All pre-analysis sampling steps (from primary sample extraction to laboratory mass reduction and handling – sub-sampling, splitting and sample preparation procedures – to the final analytical test portion extraction) play an important, often dominating role in the total uncertainty budget, which, if not included, critically affects the validity of measurement uncertainty estimates.

Most sampling errors are not included in the current MU framework, including incorrect sampling errors (ISEs), which are only defined in the theory of sampling (TOS). If ISEs are not appropriately reduced, or fully eliminated, all measurement uncertainty estimates are subject to uncontrollable and inestimable sampling bias,which is not a similar to the statistical bias because it is not constant. The sampling bias cannot, therefore, be subjected to conventional bias-correction. TOS describes why all sources of sampling bias must be competently eliminated – or sufficiently reduced (in a fully documentable way) – to make MU estimates valid. TOS provides all the theoretical and practical countermeasures required for the task.

TOS must be involved before traditional MU to provide a representative analytical aliquot; otherwise, a given MU estimate does not comply with its own metrological intentions.

The Theory of Sampling – TOS – has been established over the last 60 years as the only theoretical framework that:

i) deals comprehensively with sampling
ii) defines representativity
iii) defines material heterogeneity
iv) furthers all practical approaches needed in achieving the required representative test portion.

The starting point of every measurement process is the primary lot. All lots are characterized by significant material heterogeneity – a concept only fully acknowledged and defined by TOS – where it is crucially subdivided into constitutional heterogeneity and distributional heterogeneity (spatial heterogeneity). The heterogeneity concept (and its many manifestations) are introduced and discussed in complete detail in the pertinent literature (4-12). The full pathway from ‘lot-to-analytical-aliquot’ is complex (and in some aspects counter-intuitive because of specific manifestations of heterogeneity) and is subject to many types of uncertainty contributions in addition to analysis.

Unfortunately, the GUM (2) and EURACHEM/CITAC (3) guides focus only on estimating the total MU in a completely passive mode. TOS, on the other hand, focuses on the conceptual and practical active steps needed to minimize all sampling contributions to MU. The main thrust of our argument is that if the test portion is not representative – in other words, if all sampling error effects have not been reduced or eliminated where possible – all MU estimates are compromised. But this does not have to be the case – TOS to the fore!

The impact of heterogeneity

Proper understanding of the phenomenon of heterogeneity, its influence on sampling correctness and, most importantly, how heterogeneity can be counteracted in the sampling process requires a certain level of understanding. Here, we present a bare minimum of TOS tenets to give an appreciation of the deficiencies inherent in current MU approaches.

Before defining these concepts theoretically, Figure 1 illustrates selected examples of the many appearances of heterogeneity. In reality, heterogeneity exhibits almost infinite manifestations – a point that appears rather hopeless at first.

Heterogeneity plays out its role on all scales from constituent particles to full lot scale, and can only be fully understood by considering both constitutional and distributional aspects and characteristics. Irregular and segregated heterogeneity, for example stratification, layering, or significant individual grain irregularity, cannot be expected to follow any standard statistical distribution. Figure 1D shows a strongly heterogeneous spatial distribution – all grains with diameters above the average have been dyed blue, while all spherules with diameters below-average remain white. In this example, heterogeneity is partly physical and partly compositional because the spherules actually carry different grades/contents of the analyte in question. Compositional heterogeneity is also clear in Figure 1F: which grapes are ripe and ready for harvesting and which are not? These examples are only meant to illustrate the serious issues surrounding securing representative primary samples; there are many other examples in the literature.

Already, it should seem obvious that the notion of modeling every manifestation of heterogeneity within the fixed concepts of systematic and random variability is too simple to cover the almost infinite variations of the real world’s lot and material heterogeneity. This fact is argued and illustrated in full detail in the TOS literature. Previously, it has been argued that it is obvious that grab sampling will (always) fail in this context. Composite sampling is the only way forward (18).

For well-mixed materials (those that appear ‘homogenous’ to the naked eye, for example, Figure 1E), notions of simple random sampling have often been thought to lend support to the statistical assumption of systematic and random variability components; however, these comprise only a very minor proportion of materials with special characteristics, so clearly cannot be used to justify the same approach for significantly heterogeneous materials.

Theoretical analysis of the phenomenon of heterogeneity shows that the total heterogeneity of all types of lot material must be discriminated as two complements, the constitutional heterogeneity (CH) and distributional heterogeneity (DH). CH depends on the chemical and/or physical differences between individual ‘constituent units’ in the lot (particles, grains, kernels), generically termed ‘fragments’. Each fragment can exhibit any analyte concentration between 0 and 100 percent. When a lot (L) is sampled using single-increment procedures – grab sampling – CHL manifests itself in the form of a fundamental sampling non-representativity. The effect of this fundamental sampling error (FSE) – which is unavoidable using grab sampling – is the most fundamental tenet of TOS. CHL increases when the compositional difference between fragments increases; CHL can only be reduced by comminution, typically crushing.

DHL, on the other hand, reflects the irregular spatial distribution of the constituents  at all scales between the sampling tool volume and the entire lot. DHL is caused by the inherent tendency of particles to cluster and segregate locally (grouping) as well as more pervasively throughout the lot (segregation, layering) – or a combination of the two, as exemplified in the bewildering diversity of material heterogeneity in science, nature, technology and industry. DHL can only be reduced by mixing and/or by informed use of composite sampling with a tool that allows a high number of increments (4, 8, 11-13).

It is rarely possible to carry out forceful mixing of an entire primary lot. Therefore, if sampling lots have a high DHL, there is a very high likelihood for significant primary sampling errors: FSE + a grouping and segregation error (GSE). That is, of course, unless you pay close attention to the full complement of TOS principles.

The good news is that once you have acknowledged the principles of TOS, they are applicable to all stages and operations from the lot scale to the laboratory – representative sampling is scale-invariant. Lots come in all forms, shapes and sizes spanning the whole gamut of at least eight orders of magnitude, from microgram aliquots to million ton industrial or natural system lots.

It is critical to note that DHL is not a permanent, fixed property of the lot; GSE effects cannot be reliably estimated, as the spatial heterogeneity varies in both space and time as lots are manipulated, transported, on- and off-loaded, and so on. DHL can be changed intentionally (reduced) by forceful mixing, but can also be altered unintentionally, for example, by transportation, material handling or even by laboratory bench agitation.

An essential insight from TOS is that it is futile to estimate DHL based on assumptions of constancy. TOS instead focuses on the necessary practical counteracting measures that will reduce GSE as much as possible (the goal is full elimination) as an integral part of the sampling and sub-sampling process. In reality, it is rarely possible to completely eliminate GSE effects but they can always be brought under sufficient quantitative control (15).

Most materials in science, technology and industry are demonstrably not composed of many identical units. Instead the DHL irregularity is overwhelming (the illustrations in Figure 1 only show the tip of the iceberg). Lot heterogeneity (CHL + DHL), especially DHL, is simply too irregular and erratic to be accounted for by traditional statistical approaches that rely on systematic/random variability. In fact, this issue constitutes the primary difference between TOS and MU.

Representative sampling in practice

The focus of TOS is not on ‘the sample’ but exclusively on the sampling process that produces the sample – a subtle distinction with very important consequences. Without specific qualification of the sampling process, it is not possible to determine whether a particular sample is representative or not. Loosely referring to ‘representative samples’ without fully described, understandable and documented lot provenance and sampling processes is an exercise in futility. We repeat: a sampling process is either representative or it is not representative; there is no declination possible of this adjective.

The primary requirement in this context is sampling correctness, which means elimination of all bias-generating errors, termed ‘incorrect sampling errors’ (ISE) in TOS. After meeting this requirement (using only correct sampling procedures and equipment), the main thrust in TOS is to ensure an equal likelihood for all increments of the lot to be selected and extracted as part of an increment. This is called the ‘Fundamental Sampling Principle’ (FSP), without which all chances of representativity are lost. FSP underlies all other matters in TOS.

A unified approach for valid estimation of the sum of all sampling errors (TSE) and all analytical errors (TAE) was recently presented in the form of a new international standard, ‘DS 3077 Representative Sampling - HORIZONTAL standard’ (15). This standard analyzes the general sampling scenario comprehensively, especially how heterogeneity interacts with the sampling process and what to do about it.

A call for integration

We have shown that MU is not a fully comprehensive, universal, nor guaranteed approach to estimate a valid total measurement uncertainty if it does not include all relevant sampling effects. Around 60 years of theoretical development and application of TOS practice have shown that sampling, sample handling and sample preparation processes are associated with significantly larger uncertainty components, TSE, than the analysis (measurement) itself, TAE, typically multiplying total analytical error (TAE) by 10-50 times, dependent on the specific lot heterogeneity and sampling process in question. Occasional, very special deviations from this scenario cannot be generalized.

While GUM focuses on TAE only, the EURACHEM guide does point out some of the potential sampling uncertainty sources, but does not provide sampling operators with the necessary means to take appropriate actions. Only TOS specifies which types of errors can – and should – be eliminated (incorrect sampling errors, ISE) and which cannot, but which must instead be minimized (‘correct sampling errors’, CSE); our critique (1) crucially shows how!

Strikingly, the MU literature does not allow for sufficient understanding of the heterogeneity concept (CHL and DHL) or acknowledges the necessary practical sampling competence, both of which are essential for representative sampling. Incorrect sampling errors are non-existent in the MU framework, and the grouping and segregation error is only considered to an incomplete extent, leaving the TAE and the fundamental sampling error as the only main sources of measurement uncertainty here.

Also, the critically important sampling bias is only considered to a limited extent and only based on assumptions of statistical constancy. However, the main feature of the sampling bias is its very violation of constancy, which follows directly from a realistic understanding of heterogeneity. The only scientifically acceptable way to deal with the sampling bias is to eliminate it, as has been the main tenet of TOS since its inception in 1950 by its founder Pierre Gy (see sidebar). Here lies the major distinction between TOS and MU: TOS states that the sampling bias is a reflection of the incorrect sampling error effects interacting with a specific heterogeneity, whereas MU limits itself to acknowledging a statistical (constant) bias resulting from systematic effects attributable to protocols or people only (1).

MU is a top-down approach that is dependent upon an assumed framework of random and constant systematic effects (wrong), so individual uncertainty sources, such as GSE and ISE, are not subject to separate identification, concern, estimation, nor appropriate action (elimination/reduction). Indeed, the full measure of uncertainty sources connected to sampling, TSE, are almost completely disregarded in the MU approach. It is simply assumed that the analytical sample, which ends up as the test portion, has been extracted and mass reduced in a representative fashion. But if this assumption does not hold up, the uncertainty estimate of the analyte concentration is invalid; it will unavoidably be too small by an unknown, but significant (and variable) degree. The very different perspectives offered by MU and TOS are in serious need of clarification and reconciliation.

To that end, we call for an integration of TOS with the MU approach, illustrated by Figure 2, which shows three interconnected fishbone diagrams representing sampling, sample preparation and the standard complement of measurement uncertainty sources. Note that the intermediary complement represents the specific sample preparation error types, vividly illustrated and commented upon in a recent article in The Analytical Scientist (16).

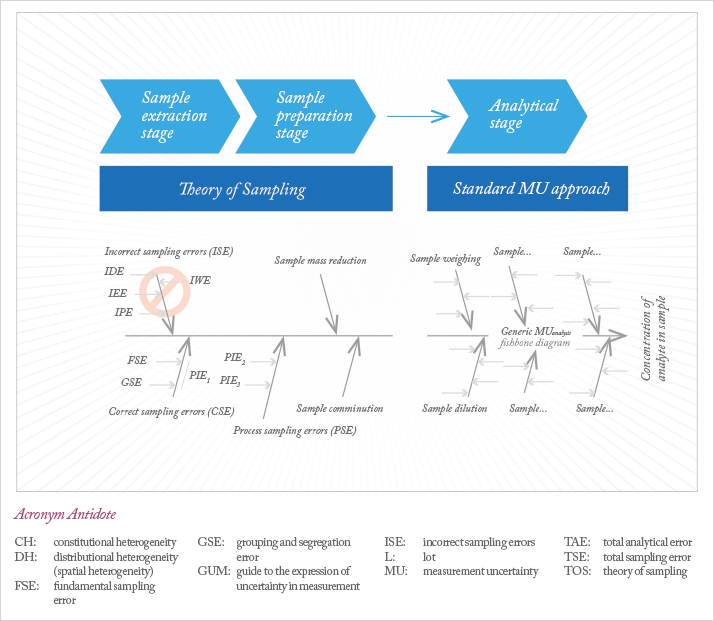
To prevent underestimation of active uncertainty sources, we must integrate the effects of all three components (sample extraction stage, sample preparation stage and analytical stage), which can actually be done in a seamless fashion; there is no need to change the current framework for MUanalysis only to acknowledge the critical role played by TOS, which is to say, the framework for MUsampling.. These sampling and sample preparation branches should be implemented in every MU framework, as sampling uncertainty contributions logically must be dealt with ahead of the traditional measurement uncertainties. In this scheme, TOS delivers a valid, representative analytical aliquot (the horizontal arrow in Figure 2) as a basis for the now valid MUanalysis estimation.

An end to the debate?

Hopefully, we have explained the critical deficiencies in MU and have shown that TOS should be introduced as an essential first part in the complete measurement process framework, taking charge and responsibility of all sampling issues at all scales – along the entire lot-to-aliquot process. We want to see a much-needed reconciliation between two frameworks that have, for too long, been the subject of quite some antagonism. Indeed, the ‘debate’ between the TOS and MU communities has at times been unnecessarily hard, but we may add that such hostilities have been unilateral (always directed towards TOS). A ‘representative (!) example of this quite unnecessary confrontation can be appreciated in the appendix of a recent doctoral thesis (17).

Squabbling aside, we hope that our efforts are seen as a call for constructive integration of TOS and MU, and look forward to comments from the wider community.

Kim H. Esbensen is a research professor at the Geological Survey of Denmark and Greenland, Copenhagen, Denmark, and Claas Wagner is an energy and environmental consultant and specialist in feed and fuel QA/QC.

Pierre Gy and the History of TOS

Pierre Gy was born in Paris in 1924. He obtained a Masters degree in chemical engineering (1956), a PhD in physics (1960) and another PhD in mathematical statistics in 1975. Pierre has been awarded four major international scientific organization awards, including two gold medals from the Société de l‘industrie minérale, and the Lavoisier Medal.

A special issue of “Chemometrics and Intelligent Laboratory Systems” was dedicated to the scholar’s distinguished achievements in science and technology: “50 years of the Theory of Sampling (TOS)” (7), which includes a tribute to Pierre Gy that summarizes his scientific career; a three-paper series: “Sampling of particulate materials I-III” ; as well as “50 years of sampling theory – a personal history”; and a listing of his complete scientific oeuvre – the latter five comprise the last professionally published papers from the pen of Pierre himself. In it, he outlines the complex history and the reason behind the development of TOS in a fascinating web of personal, scientific and industrial stories. The special issue also forms the proceedings of the First World Conference on Sampling and Blending (WCSB1), which was dedicated to the 50-year anniversary.